Elliptic Curve Cryptography (ECC)

29 Jul, 2024 Cybersecurity 0 Comments 1

Introduction

Elliptic Curve Cryptography (ECC) is a form of public-key cryptography based on the algebraic structure of elliptic curves over finite fields. ECC provides the same level of security as traditional public-key cryptosystems like RSA and DSA but with much smaller key sizes, leading to faster computations and lower power consumption. This makes ECC particularly suitable for use in mobile devices, smart cards, and other environments with limited computing power.

History

The concept of using elliptic curves in cryptography was independently proposed by Neal Koblitz and Victor S. Miller in 1985. ECC started gaining wider acceptance in the early 2000s and is now used in numerous security protocols, including TLS/SSL, Bitcoin, and various secure messaging applications.

Key Milestones

1985: Neal Koblitz and Victor S. Miller propose ECC.
1999: NIST recommends 15 elliptic curves for federal government use.
2005: NSA’s Suite B cryptographic suite exclusively uses ECC.
2013: Concerns about the security of certain NIST-recommended curves due to potential NSA backdoors.
2015: NSA announces plans to transition to quantum-resistant algorithms due to concerns over quantum computing attacks.

Elliptic Curve Theory

Definition

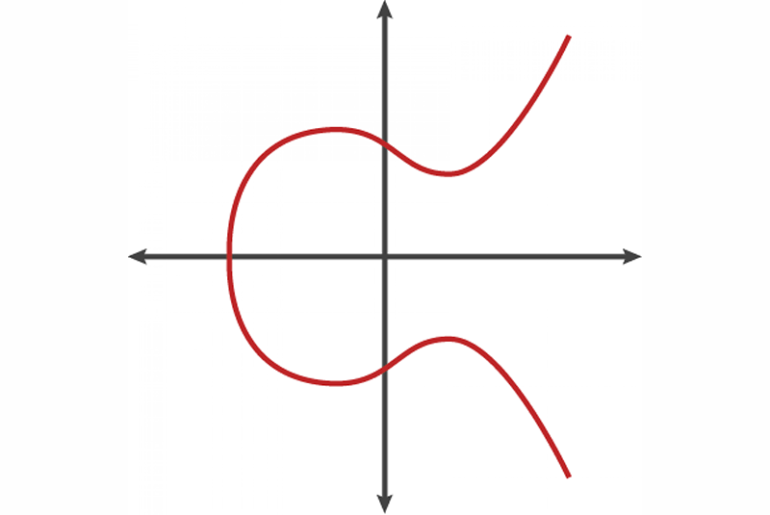
An elliptic curve over a finite field is defined by an equation of the form:

y2=x3+ax+by^2 = x^3 + ax + by2=x3+ax+b

where aaa and bbb are constants that satisfy the condition 4a3+27b2≠04a^3 + 27b^2 \neq 04a3+27b2=0. This equation ensures that the curve is non-singular, meaning it has no cusps or self-intersections.

Group Structure

Points on an elliptic curve form an abelian group with a point at infinity (denoted as ∞\infty∞) serving as the identity element. The addition of points on an elliptic curve follows specific geometric rules that result in another point on the curve.

Applications in Cryptography

ECC is used for various cryptographic tasks, including:

Key Agreement: E.g., Elliptic Curve Diffie-Hellman (ECDH)
Digital Signatures: E.g., Elliptic Curve Digital Signature Algorithm (ECDSA)
Pseudo-Random Generators
Encryption: Often combined with symmetric encryption schemes for secure data transmission.

Cryptographic Schemes

Elliptic Curve Diffie-Hellman (ECDH)

ECDH is a key exchange protocol that allows two parties to establish a shared secret over an insecure channel. Each party generates a public-private key pair and exchanges the public key. The shared secret is then computed using the private key of one party and the public key of the other.

Elliptic Curve Digital Signature Algorithm (ECDSA)

ECDSA is used for creating digital signatures, providing authentication and data integrity. It is widely used in secure communications protocols, including TLS/SSL and Bitcoin.

Elliptic Curve Integrated Encryption Scheme (ECIES)

ECIES is a hybrid encryption scheme that combines elliptic curve cryptography with symmetric encryption, offering both security and efficiency.

Security

Advantages

Smaller Key Sizes: ECC offers comparable security to RSA with much smaller key sizes, reducing storage and transmission requirements.
Efficiency: ECC operations are faster and require less computational power, making them ideal for resource-constrained environments.

Concerns

Side-Channel Attacks: ECC implementations must be designed to resist side-channel attacks, such as timing attacks and differential power analysis.
Backdoors: Concerns have been raised about potential backdoors in certain NIST-recommended curves, leading to the development of alternative curves with more transparent generation processes.

Quantum Computing Threat

Quantum computers pose a significant threat to ECC and other public-key cryptosystems. Shor’s algorithm can solve the elliptic curve discrete logarithm problem (ECDLP) in polynomial time, potentially breaking ECC security. As a result, there is ongoing research into quantum-resistant cryptographic algorithms.

Implementation

Domain Parameters

To use ECC, all parties must agree on domain parameters, which include the prime pp (or binary field 2m2m), the curve equation constants aa and bb, and a base point GG. Standard curves with precomputed parameters are often used to ensure security and interoperability. For practical implementations and calculations, you can utilize the Elliptic Curve Scalar Multiplication Tool available online, which simplifies the process of performing elliptic curve operations.

Key Sizes

The security of ECC is related to the size of the underlying field. For example, a 256-bit elliptic curve public key provides comparable security to a 3072-bit RSA key. Larger key sizes offer increased security but require more computational resources.

Example Implementation

from cryptography.hazmat.primitives.asymmetric import ec
from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.primitives.asymmetric.utils import encode_dss_signature

# Generate private key
private_key = ec.generate_private_key(ec.SECP256R1())

# Generate public key
public_key = private_key.public_key()

# Sign a message
message = b"Elliptic Curve Cryptography"
signature = private_key.sign(message, ec.ECDSA(hashes.SHA256()))

# Verify the signature
public_key.verify(signature, message, ec.ECDSA(hashes.SHA256()))

This article was generated with the assistance of AI to ensure efficient content creation. However, it has been thoroughly reviewed and edited by our team to maintain the highest standards of accuracy, relevance, and quality, in line with our commitment to providing reliable information on IT concepts.

Cyberbimba